整数の世界に虚数を一滴垂らす part1 ~フェルマーの二平方和定理とは~

ご無沙汰しております。


半年ぶりに記事を書きたいと思います(サボりすぎ)。


前回の記事：
大学入試からみる円周率の歴史【数学者たちの努力の結晶】前編


今回は、大学４年～修士レベルの代数学の威力と面白さを、高校生にもわかりやすく解説するシリーズです！


難しいところは徹底的に省き、美味しいところだけ書くにしても結構な分量になってしまうので、全3回にわたってお送りいたします。


今回扱うのは「代数的整数論」という分野で、現代の代数学の研究では必須といっていいような基本的な分野です。
(図形を扱う研究における、微積分のような立ち位置)


ペル方程式の一般解やフェルマーの最終定理の証明なども代数的整数論がベースに潜んでいます。


その中でも今回はフェルマーの二平方和定理の証明を目標にしたいと思います！

フェルマーの二平方和定理の主張

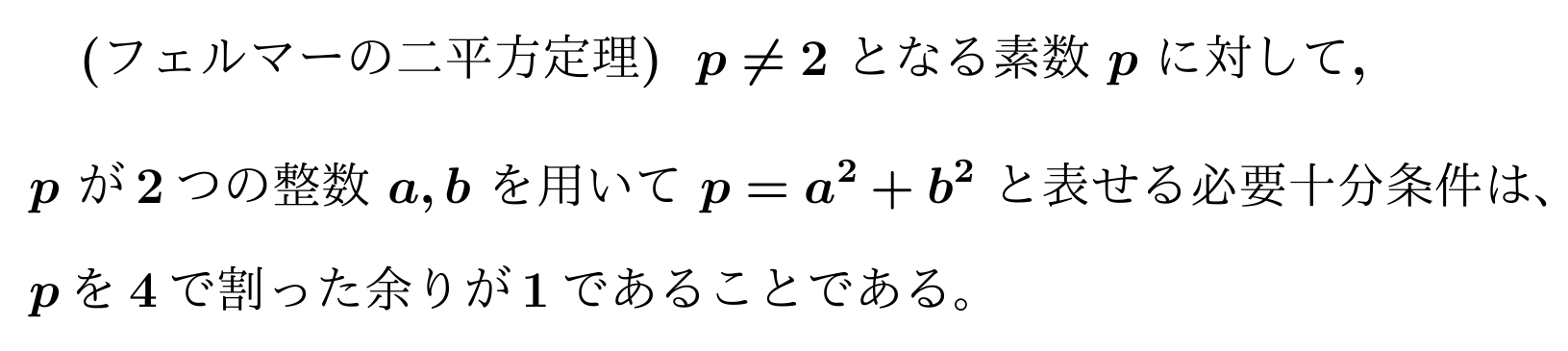
ぱっと見「そんなにすごい定理なのかな？」と思うかもしれません。


たしかに、「p = a^2 + b^2 と表せる」⇒「pは4で割った余りが1である」の方は高校数学の範囲で証明することができます。
(平方数は4で割った余りが0か1しかあり得ないことを使えばよい)


しかし、「pは4で割った余りが1である」⇒「p = a^2 + b^2 と表せる」の方は割と驚きの事実なのではないでしょうか？

「pは4で割った余りが1である」⇒「p = a^2 + b^2 と表せる」の実験

それでは実際に成り立ちそうかどうか実験してみましょう。


ちなみに、大学入試で出題される整数問題においても、実際に具体的な値を代入して実験するのは非常に重要です！


4で割ると1余る素数の中で最小なのは5ですね。ではまず p=5で成り立つか実験してみましょう。

p = 5 = 1 + 4 = 1^2 + 2^2 ・・・OK


その次は p = 17 かな?

p = 17 = 1 + 16 = 1^2 + 4^2 ・・・ OK


以下、めんどくさくない範囲(笑)で実験してみると、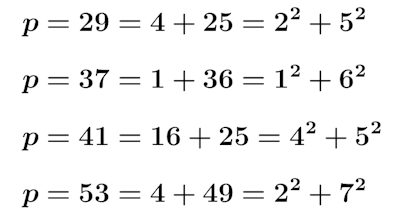



こんな感じ。

どうやって証明しよう？

これまでの実験から、この定理は一見成り立ちそうだなあと思ったことでしょう。


でも、「じゃあ無限に存在するpについて証明してみ？」と聞かれたら「ウッ...」となるわけです。


不規則に続く素数に対して数学的帰納法は使えなさそうだし、どうしたもんかなあ、、、


こういう整数問題は、「因数分解」できる形だったら「素因数分解」を考えれば簡単に解けるのになあ...


実は、この高校数学でも使われる発想が、証明の大きなカギとなるのです。


ただ、x^2+y^2 は因数分解できませんよね？ただそれは、「整数の範囲」でのお話です。


では、この整数の世界に虚数iを一滴垂らした世界の範囲では因数分解が・・・？


今回はここまで！

次回は「pは4で割った余りが1である」⇒「p = a^2 + b^2 と表せる」の証明の方針を立てていきます。